This blog post covers intended solutions of two crypto challenges from InCTF-2018: Request-Auth and EC-Auth.

Request-Auth

Challenge Description

This was a medium level crypto challenge that I created for InCTF International-2018. In the challenge you are given multiple files: iv.txt, key.enc, publickey.pem, ServerSide.py, session.enc and also have a service running these files.

Contents of ServerSide.py:

#!/usr/bin/env python2.7

from Crypto.Cipher import AES
from Crypto.PublicKey import RSA
from Crypto.Util.number import *
from os import urandom
import sys

BLOCKSIZE = 16

class Unbuffered(object):
   def __init__(self, stream):
       self.stream = stream
   def write(self, data):
       self.stream.write(data)
       self.stream.flush()
   def writelines(self, datas):
       self.stream.writelines(datas)
       self.stream.flush()
   def __getattr__(self, attr):
       return getattr(self.stream, attr)

sys.stdout = Unbuffered(sys.stdout)

class colors:
    reset='\033[0m'
    red='\033[31m'
    green='\033[32m'
    orange='\033[33m'
    blue='\033[34m'

def unpad(s):
    s = s[:-ord(s[len(s) - 1])]
    return s

def check_valid_request(s):
    try:
        s = s.split(":")
    except:
        return False
    if len(s) != 3:
        return False
    if s[0] != "bi0s":
        return False
    if s[1][:7] != "userid=":
        return False
    if s[2][:5] != "user=":
        return False
    return True

class ServerSide:
    def __init__(self, key, iv):
        self.key = key[-16:]
        self.iv = iv[-16:]

    def process_request(self, req_enc):
        try:
            obj2 = AES.new(self.key, AES.MODE_CBC, self.iv)
            request = obj2.decrypt(req_enc)
            return check_valid_request(request)
        except:
            return False

def get_AES_key():
    try:
        key_enc = raw_input("Enter encrypted key value in hex: ")
        key_enc = int(key_enc, 16)
    except:
        print colors.red + "Enter valid input!" + colors.reset
        sys.exit()
    priv_key = RSA.importKey(open("privatekey.pem").read())
    n, d = priv_key.n, priv_key.d
    key_AES = pow(key_enc, d, n)
    key_AES = long_to_bytes(key_AES)
    return key_AES

string1 = colors.blue + """
$$\       $$\  $$$$$$\\
$$ |      \__|$$$ __$$\\
$$$$$$$\  $$\ $$$$\ $$ | $$$$$$$\\
$$  __$$\ $$ |$$\$$\$$ |$$  _____|
$$ |  $$ |$$ |$$ \$$$$ |\$$$$$$\\
$$ |  $$ |$$ |$$ |\$$$ | \____$$\\
$$$$$$$  |$$ |\$$$$$$  /$$$$$$$  |
\_______/ \__| \______/ \_______/
""" + colors.reset
if __name__ == '__main__':
    print colors.orange + "Welcome to bi0s Request Validation Service" + colors.reset
    print string1
    key = get_AES_key()
    iv = open("iv.txt").read()
    obj1 = ServerSide(key, iv)

    try:
        ct = raw_input("\nEnter value of encrypted session request in hex: ")
        ct = ct.decode("hex")
    except TypeError:
        print colors.red + "Enter a valid hex string!" + colors.reset
        sys.exit()

    if obj1.process_request(ct) == True:
        print colors.green + "\nValid request!" + colors.reset
    else:
        print colors.red + "\nInvalid request!" + colors.reset

Okay, so the service is basically implementing a hybrid cipher- a combination of RSA and AES to authenticate session requests coming from a user and is internally using a public and a private key in this process.

ClientSide:

For every new session, client generates a new valid request
The client encrypts the request req in AES-CBC mode using a 16-byte key k and 16-byte Initialisation Vector IV: $session\_enc=E_{AES_{k, IV}}(req)$
Client then encrypts the 16-byte AES key k using public-key of the server: $key\_enc = k^e\mod n$
In the final step, user gives the encrypted session session_enc and encrypted session-key key_enc as an input to the server

ServerSide:

Server receives session_enc and key_enc from the Client.
Decrypts key_enc using it’s private key: $k=key\_enc^d\mod n$
Takes 16 least significant bytes of the resultant value of k as the key
Decrypts session_enc using value of key obtained from step-3: $req=D_{AES_{k, IV}}(session\_enc)$
Checks the validity of resultant request using check_valid_request() function.
Returns True if the request is valid, False if it isn’t.

Had I been a participant trying to solve this challenge, I would have looked at check_valid_request(). Why? Because mostly in such functions, either there is an intentional vulnerability or you can find some unintended weakness that you can exploit. Let’s move to that part:

def check_valid_request(s):
    try:
        s = s.split(":")
    except:
        return False
    if len(s) != 3:
        return False
    if s[0] != "bi0s":
        return False
    if s[1][:7] != "userid=":
        return False
    if s[2][:5] != "user=":
        return False
    return True

Doesn’t look like ^^ can be exploited. Dead end.

We know that the server only tells us if the request is valid or not, we won’t get a flag from the server directly in any case.

Either we find the server’s private key or we find the AES key using which session.enc is encrypted. We are not able to factorise N, nor are we able to find any weakness in the public key, hence the only remaining option is to find the AES key.

How do we find it?

The Vulnerability

Remember how the server inputs encrypted key and evaluates the key to be used for encryption? Check out the first three steps happening on ServerSide:

Receives session_enc and key_enc from the client.
Decrypts key_enc using it’s private key: $k=key\_enc^d\mod n$
Takes 16 least significant bytes of the resultant value of k as the key

Do you see the weakness there? Step-3! “Takes 16 least significant bytes from resultant value of k obtained after decryption“. Notice that we are in control of the encrypted AES key and hence we can do a chosen ciphertext attack. We have found the vulnerability, next question- how do we exploit it?

The Exploit

We know that: $key\_enc = k^e\mod n$

If we multiply key_enc by $2^{me}\mod n$, we will have: $$key\_enc * 2^{me} \mod n = k^e2^{me}\mod n$$ $$k^e2^{me}\mod n = (2^mk)^e\mod n$$

So, just by knowing the ciphertext of k, we can generate values of ciphertext of 2k, 4k, 8k, … and so on. We also know that no matter how big the ciphertext is, the server will just take 16 least significant bytes of k after decryption.

We will denote $key\_enc_m\equiv key\_enc*(2^m\mod n)\mod n$ and $k_m\equiv k*2^m\mod n$

Consider key_enc127 which is encryption of k127 where every bit but the most significant bit is zero. After sending key_enc127 to the server, upon decryption, only 16 least significant bytes are selected as the key for decrypting the session. This implies that k127‘s most significant bit is k’s least significant bit. We assume that k127‘s most significant bit is zero, encrypt the session with key that has least significant bit as 0 (Remaining all the bits are anyway zero) and send it to the server.

If the server responds with a “Valid Response” message, then the least significant bit of the AES key is 0, otherwise it is 1. Next, we send key_enc126 which is the encryption of k126, encrypt a valid session with key where 0-125th bits from left are zero, 126th bit is zero and 127th bit is the least significant bit of k we got from previous iteration. Again, if the server responds with a “Valid Response” message, then the second least significant bit of AES key is 0, otherwise it is 1.

We iterate this for key_enc125, key_enc124, …, key_enc0, until all the bits of k are obtained. I have implemented this step as a small python snippet:

for i in range(127, -1, -1):
    r = process("./run.sh")
    key_payload = (key_enc*pow(2, i*publickey.e, publickey.n)) % publickey.n
    key_dec = hex(int("0" + global_dec_key[::-1] + "0"*i, 2))[2:].replace("L","").zfill(32).decode("hex")
    enc_session_payload = encrypt_request("bi0s:userid=test:user=test2", key_dec, iv)
 
    # Sending the payload to the service
    send_enc_key(key_payload)
    send_enc_session(enc_session_payload)
 
    # Checking if the request is valid
    if check_enc_req_validity() == 1:
         global_dec_key += "0"
    else:
         global_dec_key += "1"
    r.close()
 
AES_session_key = hex(int(global_dec_key[::-1], 2)[2:].replace("L","").zfill(32).decode("hex")

You can check out the entire exploit script here:

from pwn import *
from Crypto.Cipher import AES
from Crypto.PublicKey import RSA
from Crypto.Util.number import *
 
def check_valid_request(s):
    try:
        s = s.split(":")
    except:
        return False
    if len(s) != 3:
        return False
    if s[0] != "bi0s":
        return False
    if s[1][:7] != "userid=":
        return False
    if s[2][:5] != "user=":
        return False
    return True
 
def pad(s):
    s += chr(16 - len(s)%16)*(16 - len(s)%16)
    return s
 
def send_enc_key(key):
    r.recvuntil("Enter encrypted key value in hex: ")
    send_key = hex(key)[2:].replace("L","")
    r.sendline(send_key)
 
def send_enc_session(enc_session):
    r.recvuntil("Enter value of encrypted session request in hex: ")
    send_session = enc_session.encode("hex")
    r.sendline(send_session)
 
def check_enc_req_validity():
    validity = r.recvuntil("!").split("\n")[1]
    if validity == "Valid request!":
        return 1
    elif validity == "Invalid request!":
        return 0
    else:
        return -1
 
def encrypt_request(request, key, iv):
    if check_valid_request(request) == False:
        print "Cannot encrypt invalid request"
        return -1
    obj1 = AES.new(key, AES.MODE_CBC, iv)
    ct = obj1.encrypt(pad(request))
    return ct
 
# Reading values from files
key_enc = bytes_to_long(open("../Handout/key.enc").read())
iv = open("iv.txt").read()
session_enc = open("../Handout/session.enc").read()
publickey = RSA.importKey(open("../Handout/publickey.pem").read())
 
# Final decrypted key
global_dec_key = ""
 
# Pre-test: should return true
r = remote("18.224.31.42","1337")
key_payload = key_enc
send_enc_key(key_payload)
send_enc_session(session_enc)
print "[+] Pre-test results: ", check_enc_req_validity()
r.close()
 
# Exploit
for i in range(127, -1, -1):
    r = remote("18.224.31.42","1337")
    key_payload = (key_enc*pow(2, i*publickey.e, publickey.n)) % publickey.n
    key_dec = hex(int("0" + global_dec_key[::-1] + "0"*i, 2))[2:].replace("L","").zfill(32).decode("hex")
    enc_session_payload = encrypt_request("bi0s:userid=test:user=test2", key_dec, iv)
 
    # Sending the payload to the service
    send_enc_key(key_payload)
    send_enc_session(enc_session_payload)
 
    # Checking if the request is valid
    if check_enc_req_validity() == 1:
         global_dec_key += "0"
    else:
         global_dec_key += "1"
    r.close()
 
AES_session_key = hex(int(global_dec_key[::-1], 2))[2:].replace("L","").zfill(32).decode("hex")
obj1 = AES.new(AES_session_key, AES.MODE_CBC, iv)
print "Here we go: ", obj1.decrypt(session_enc)

Running this script will give us the flag as: inctf{y0u_eff1ng_CCA2_w1nn3r}

Real World Example

This vulnerability and attack was a part of research[1] done on Tencent’s QQ Browser, a popular mobile browser in China with hundreds of millions of users worldwide, by three professors- Thomas Ristenpart, Jedidah R. Crandall and Jeffrey Knockel. It was quite silly yet critical vulnerability in QQ Browser that they found. A small excerpt from the paper:

When users run QQ Browser on Android, it makes a se- ries of what QQ Browser interally terms as “WUP re- quests” to QQ Browser’s server. These WUP requests contain information such as a user’s International Mobile Equipment Identifier (IMEI), International Mobile Sub- scriber Identification (IMSI), QQ username, WiFi MAC address, SSID of connected WiFi access point and of all in-range access points, Android ID, URLs of all web- pages visited, and other private information.

These requests were encrypted using a method similar to that in the challenge “Request-Auth” with the same vulnerability (No padding and selecting only the least 16 bytes as the key) . This was a critical vulnerability as an attacker can decrypt any session and get access to personal, sensitive information stored in the request (IMEI, QQ username, WiFi MAC address, URLs of all web pages visited etc.)

[1] https://arxiv.org/abs/1802.03367

YCombinator news: https://news.ycombinator.com/item?id=16362488

It was after this paper got released, I decided to create a challenge based on it! Hope you enjoyed the challenge and the write-up! In case you have any queries or suggestions regarding the solution/write-up, you can reach me out on Twitter, or comment in the comments section below!

Challenge Description

This was a crypto challenge based on Elliptic Curves that I created for InCTF-International 2018. In this challenge you are given two files: ecauth.py and ecsession.py, ecauth.py is basically a file implementing all the operations related to the Elliptic Curve (Point Addition, Scalar Multiplication): $y^2\equivx^3+a*x+b\mod p$

This challenge requires basic knowledge of Elliptic Curves to understand. In case you are not familiar with Elliptic Curves and want to learn, here are a few resources that can help you:

I took ecauth.py from https://bitcointalk.org/index.php?topic=23241.0 and modified it for the challenge. The modified part is:

class Public_key(object):
    def __init__(self, generator):
        self.generator = generator
        self.curve = generator.curve()
        n = generator.order()
        if not n:
            raise RuntimeError("Generator must have order")
        if not n * generator == INFINITY:
            raise RuntimeError("Generator point order is bad")
        if generator.x() < 0 or n <= generator.x() or  generator.y() < 0 or n <= generator.y():
            raise RuntimeError("Generator point has x or y out of range")
 
    def check(self, point):
        k = self.generator.order()
        if not k:
            raise RuntimeError("Generator must have order")
        if not k * point == INFINITY:
            raise RuntimeError("Generator point order is bad")
        if point.x() < 0 or k <= point.x() or  point.y() < 0 or k <= point.y():
            raise RuntimeError("Generator point has x or y out of range")
 
    def _verify(self, handshake):
        P = self.generator
        Q = handshake.Q
        R = handshake.R
        s = handshake.s
        try:
            self.check(Q)
            self.check(R)
        except:
            return False
        if (s*P).x() == (Q+R).x() and (s*P).y() == (Q+R).y():
            return True
        else:
            return False
 
class Private_key(object):
    def __init__(self, public_key, x):
        self.public_key = public_key
        self.privkey = x
 
    def _sign(self, r):
        P = self.public_key.generator
        Q = self.privkey * P
        R = r * P
        s = self.privkey + r
        return Handshake(Q, R, s)

Let us analyse ecsession.py to understand things further:

#!/usr/bin/env python2.7
 
from Crypto.Util.number import *
from os import urandom
import sys
import ecauth
from secret import flag, n
 
class Unbuffered(object):
   def __init__(self, stream):
       self.stream = stream
   def write(self, data):
       self.stream.write(data)
       self.stream.flush()
   def writelines(self, datas):
       self.stream.writelines(datas)
       self.stream.flush()
   def __getattr__(self, attr):
       return getattr(self.stream, attr)
 
sys.stdout = Unbuffered(sys.stdout)
 
class colors:
    reset='\033[0m'
    red='\033[31m'
    green='\033[32m'
    orange='\033[33m'
    blue='\033[34m'
 
p = 89953523493328636138979614835438769105803101293517644103178299545319142490503
a = p-3
b = 28285296545714903834902884467158189217354728250629470479032309603102942404639
ec = ecauth.CurveFp(p, a, b)
 
# Point P on the curve
_Px = 0x337ef2115b4595fbd60e2ffb5ee6409463609e0e5a6611b105443e02cb82edd8L
_Py = 0x1879b8d7a68a550f58166f0d6b4e86a0873d7b709e28ee318ddadd4ccf505e1aL
 
# n is the order of the subgroup generated by (_Px, _Py)
assert ec.contains_point(_Px, _Py)
 
# x is the session-secret key
x = getPrime(254)
 
assert x < n
 
point_P = ecauth.Point(ec, _Px, _Py, n)
assert point_P * n == ecauth.INFINITY
 
publickey = ecauth.Public_key(point_P)
privatekey = ecauth.Private_key(publickey, x)
 
"""
You can use the _sign method in ecauth to sign for authentication process.
But remember,
You must have the same x as generated in this script to successfully authenticate!
"""
 
print colors.orange + "-"*26 + "Welcome to EC-Auth mechanism" + "-"*26 + colors.reset
point_Q = x * point_P
print "\nHere is my point Q = x * P: ", point_Q
 
try:
    _Rx = raw_input("\nGive me x-coordinate of point R = r * P (in hex without 0x): ")
    _Ry = raw_input("Give me y-coordinate of point R = r * P (in hex without 0x): ")
    s = raw_input("Give me s = r + x (in hex without 0x): ")
    _Rx = int(_Rx, 16)
    _Ry = int(_Ry, 16)
    s = int(s, 16)
except:
    print colors.red + "\nEnter proper hex values!" + colors.reset
    sys.exit()
 
if not ec.contains_point(_Rx, _Ry):
    print colors.red + "\nPoint R does not lie on the curve!" + colors.reset
    sys.exit()
 
point_R = ecauth.Point(ec, _Rx, _Ry)
assert n * point_R == ecauth.INFINITY
 
obj1 = ecauth.Handshake(point_Q, point_R, s)
if publickey._verify(obj1):
    print colors.green + "\nHere, take your flag: " + flag + colors.reset
else:
    print colors.red + "\nI knew you would fail" + colors.reset
    sys.exit()

The script is trying to implement an authentication service similar to this:

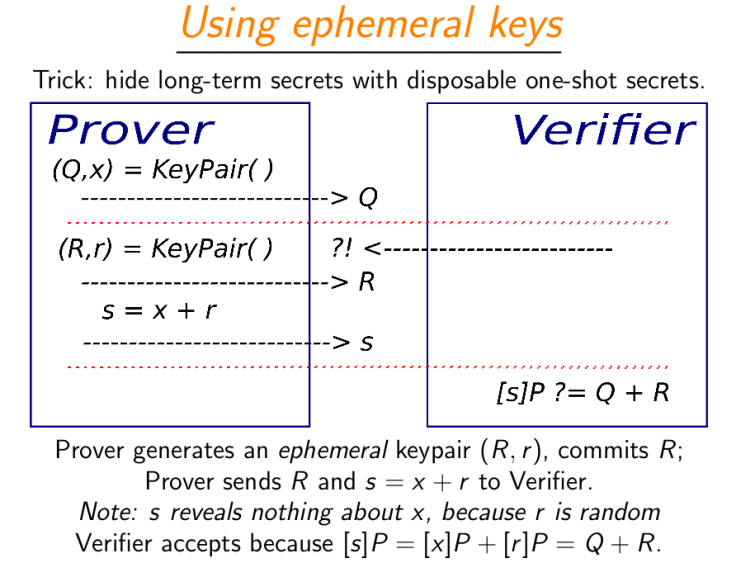
Since I could not think of ways in which the attacker would intercept such a communication in order to exploit it, I modified the above authetication process (keeping the concept as it is):

The curve used for the process is $y^2\equiv x^3+a*x+b\mod p$, where p = 89953523493328636138979614835438769105803101293517644103178299545319142490503, a = p-3, and b = 28285296545714903834902884467158189217354728250629470479032309603102942404639
Server takes a point on the curve P=(_Px, _Py), where _Px = 0x337ef2115b4595fbd60e2ffb5ee6409463609e0e5a6611b105443e02cb82edd8L, _Py = 0x1879b8d7a68a550f58166f0d6b4e86a0873d7b709e28ee318ddadd4ccf505e1aL
Server generates point Q = x * P (consider it similar to a Prover generating Q and x is the secret key generated by the Prover using a pseudo random number generator) and gives the coordinates of Q.
The next step is intrusion of communication channel, so you being the attacker will have to give coordinates of R = r * P. If you are the prover, then you will have the value of r, but you are an attacker, so generating R such that the authentication passes, is the challenge 😉
After getting the value of R, server asks the value of s = x + r, which you can give as input. Again, you are not the prover (you won’t have the values of x and r, so the challenge again is, how do you get it?)
Then the server calculates if s*P = Q + R, and returns the flag in case it evaluates to true, otherwise simply returns false
- This will be true in case you are the prover because for true values of x and r, $s*P=(x+r)*P=(x*P)+(r*P)=Q+R$

How can we accomplish this, as an attacker?

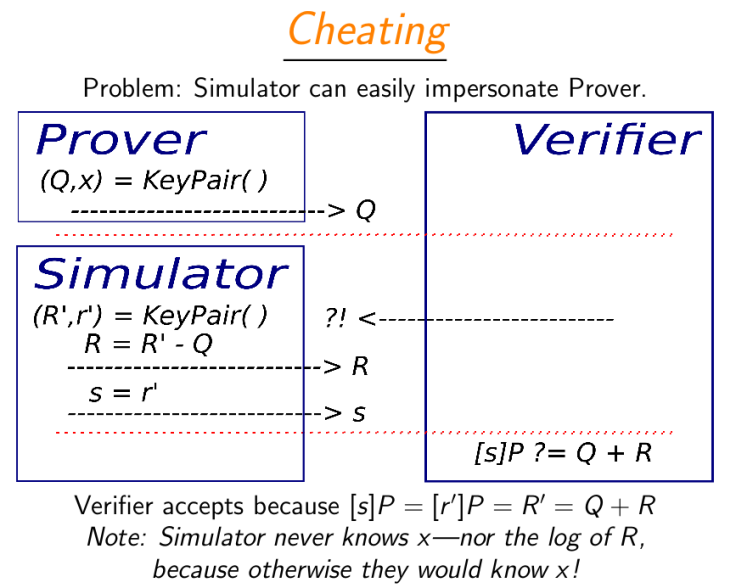
Reference: https://ecc2017.cs.ru.nl/slides/ecc2017school-smith.pdf

import ecauth
from Crypto.Util.number import *
 
p = 89953523493328636138979614835438769105803101293517644103178299545319142490503
a = p-3
b = 28285296545714903834902884467158189217354728250629470479032309603102942404639
ec = ecauth.CurveFp(p, a, b)
 
# Point P on the curve
_Px = 0x337ef2115b4595fbd60e2ffb5ee6409463609e0e5a6611b105443e02cb82edd8L
_Py = 0x1879b8d7a68a550f58166f0d6b4e86a0873d7b709e28ee318ddadd4ccf505e1aL
 
# Order of the subgroup generated by (_Px, _Py)
n = 89953523493328636138979614835438769106005948670998555217484157791369906305783
assert ec.contains_point(_Px, _Py)
 
point_P = ecauth.Point(ec, _Px, _Py, n)
assert point_P * n == ecauth.INFINITY
 
list_a = raw_input("Enter coordinates of Q: ").split(",")
print list_a
_Qx = int(list_a[0])
_Qy = int(list_a[1])
 
assert ec.contains_point(_Qx, _Qy)
negative_Q = ecauth.Point(ec, _Qx, -_Qy, n)
 
r_prime = getPrime(254)
R_prime = r_prime * point_P
 
print hex((R_prime + negative_Q).x())[2:].replace("L","")
print hex((R_prime + negative_Q).y())[2:].replace("L","")
print hex(r_prime)[2:].replace("L","")

The output of this script, when given to the server as an input, gives us the flag: inctf{D4nger0us_eph3m3ral_k3ys!}

Last year, around November I got a chance to learn Elliptic Curves at ECC Winter School, Nijmegen. It was after coming from there that I decided to make a challenge based on Ephemeral Keys (The attack was discussed in one of the sessions, taken by Benjamin Smith: https://ecc2017.cs.ru.nl/school.shtml, hence picture references to the slides ;)). I am and will always be grateful to the organising committee for giving me this opportunity and scholarship. Thanks!

Hope you enjoyed the challenge! If you have any queries related to any crypto challenge from InCTF International you can put it in the comments section, or ping me on Twitter!

Request-Auth#

The Vulnerability#

The Exploit#

Real World Example#

Request-Auth

The Vulnerability

The Exploit

Real World Example