Hack.lu CTF is over and we (@teambi0s) finished 13th globally and since we were registered as a local team (thanks to @GeethnaTk) and stood first among the teams registered locally, hence we are eligible for prizes! Yay!
This blog post covers detailed solutions to two of the crypto challenges from Hack.lu CTF 2018- Relations and Multiplayer Part-1. While the former was just about guessing (or detecting the pattern, whatever you want to say) of a black box encryption service, the latter was a more interesting challenge involving Elliptic Curves.
To sum up, I enjoyed solving the crypto challenges this year, but I felt kinda sad and frustrated when Multiplayer Part-2 got removed because of some issues, as I spent quite a lot of time trying it. I learnt a lot meanwhile, so I guess it was worth it!
Kudos to the organisers for putting up a beautiful CTF! Let us move onto the solutions now 🙂
Relations
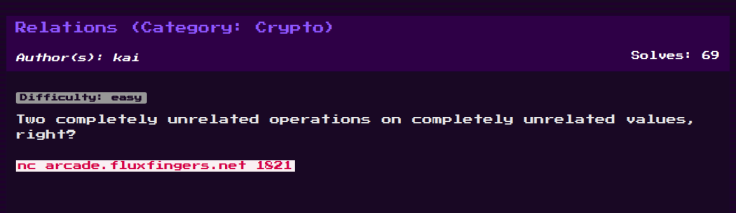
This was a fairly easy challenge although we are not given any encryption script. We are given three operations on the nc service to choose, XOR, ADD and DEC (decrypt). Then, we have to give an input string on which the selected operation is done.
How the operation takes place was unknown at that particular point of time. But we see something strange here:
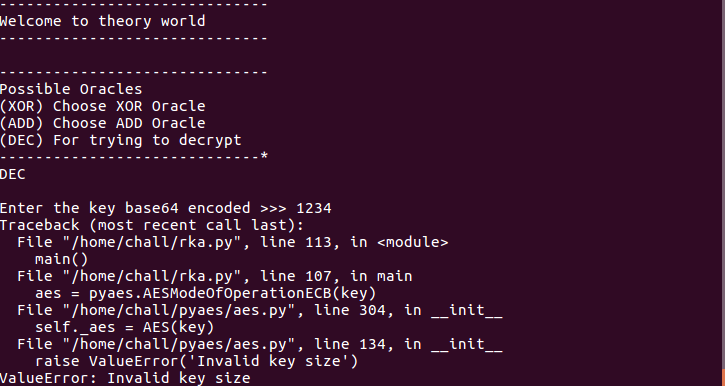
So now we know that DEC operation takes in base64 key which it then uses to AES decrypt some string, which could possibly be our flag.
Then, we started giving random inputs to XOR and ADD operations and my teammates noticed this:
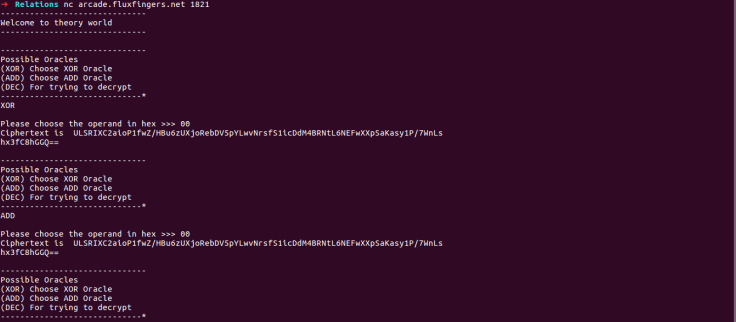
For the same input 00, ADD and XOR operations give the same output! I immediately thought that we can use this to leak out the string to which our input is XORed or ADDed. And that string could possibly be the key used as an input in DEC to AES decrypt our flag. How can we exploit this?
Consider A, B of size 1-bit each. If A=1, A xor B and A+B will be equal only when B = 0. That’s it! We can use this property to generalise and get all the bits of the key:
- Send \(2^0, 2^1, 2^2,…, 2^{127}\) as inputs for both XOR and ADD and check if the outputs for XOR and ADD for an input match.
- If they match, then add 0 to the binary keystring, otherwise add 1.
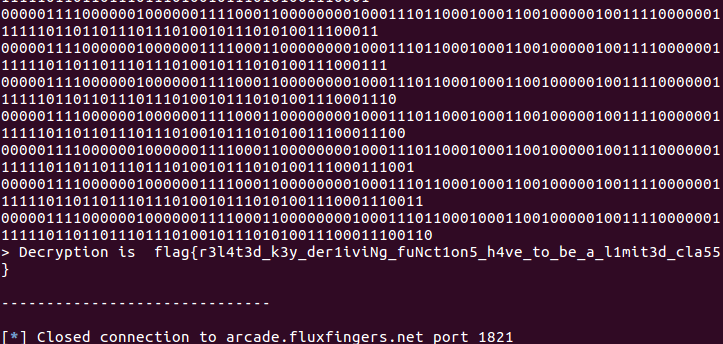
I wrote the following script to implement this attack:
from pwn import *
import string
def choose_XOR_op(input):
for i in input:
assert i in string.hexdigits
r.recvuntil("*")
r.sendline("XOR")
r.recvuntil(">>")
r.sendline(input)
ct = r.recvline()[17:].strip()
unknown = r.recvline().strip()
return ct, unknown
def choose_ADD_op(input):
for i in input:
assert i in string.hexdigits
r.recvuntil("*")
r.sendline("ADD")
r.recvuntil(">>")
r.sendline(input)
ct = r.recvline()[17:].strip()
unknown = r.recvline().strip()
return ct, unknown
def choose_DEC_op(input):
r.recvuntil("*")
r.sendline("DEC")
r.recvuntil(">>")
r.sendline(input)
print r.recvline()
print r.recvline()
r.close()
list1 = [2**i for i in range(128)]
key = ""
r = remote("arcade.fluxfingers.net","1821")
for i in list1:
ct, unknown = choose_XOR_op(hex(i)[2:].replace("L",""))
ct1, unknown1 = choose_ADD_op(hex(i)[2:].replace("L",""))
if ct+unknown == ct1+unknown1:
key += "0"
print key
else:
key += "1"
print key
key = hex(int(key[::-1], 2))[2:].replace("L","").decode("hex").encode("base64").replace("\n","")
choose_DEC_op(key)
r.close()
And got the flag!
Multiplayer Part-1
Note: This challenge requires basic knowledge of Elliptic Curves. In case you don’t know ECC and want to start, you can use the following resources:
- http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
- https://github.com/ashutosh1206/Crypton/tree/master/Elliptic-Curves
In this challenge, we are given the following files: server.sage, parameters.sage and points.db. We can host the challenge locally using server.sage to test our exploit. Having a glance at the challenge description quickly reveals that this challenge is based on Elliptic Curves which is quite evident from parameters.sage as well:
param = { "hacklu":
((889774351128949770355298446172353873, 12345, 67890),
# Generator of Subgroup of prime order 73 bits, 79182553273022138539034276599687 to be excact
(238266381988261346751878607720968495, 591153005086204165523829267245014771),
# challenge Q = xP, x random from [0, 79182553273022138539034276599687)
(341454032985370081366658659122300896, 775807209463167910095539163959068826)
)
}
serverAdress = '0.0.0.0'
serverPort = 23426
(p, a, b), (px, py), (qx, qy) = param["hacklu"]
E = EllipticCurve(GF(p), [a, b])
P = E((px, py))
Q = E((qx, qy))
def is_distinguished_point(p):
return p[0] < 2^(100)
So the curve defined is \(y^2\equiv x^3 + a*x + b\mod p\), where
p = 889774351128949770355298446172353873
a = 12345
b = 67890
Also, \(P\) and \(Q\) are two points on this curve where \(Q = x*P\) (Note that * symbol here signifies Scalar Multiplication and x is the secret key whose value is unknown),
P = (238266381988261346751878607720968495, 591153005086204165523829267245014771)
Q = (341454032985370081366658659122300896, 775807209463167910095539163959068826)
We are also given order of the subgroup generated by \(P\):
79182553273022138539034276599687
According to the property of Elliptic Curves: \(n*P = 0\), where \(n\) is the order of the subgroup generated by a point \(P\) on an Elliptic Curve.
The service communicates with the user using JSON request and JSON responses only. Let us analyse some code snippets below that are taken from server.sage.py.
DLogHandler class:
class DLogHandler(asyncore.dispatcher_with_send):
def handle_read(self):
try:
json_data = self.recv(_sage_const_8192 )
if not json_data:
return
data = json.loads(json_data)
# check if the format is correct
if not ("x" in data and "y" in data and "c" in data and "d" in data and "groupID" in data):
response = json_response(_sage_const_3 )
else:
c = Integer(data["c"])
d = Integer(data["d"])
x = Integer(data["x"])
y = Integer(data["y"])
X = E((x, y))
if X == c*P + d*Q:
response = get_response(data["x"], data["y"], data["c"], data["d"], data["groupID"])
else:
print("expected %s = %d*%s + %d*%s, but got %s" % (c*P + d*Q, c, P, d, Q, X))
response = json_response(_sage_const_4 )
self.send(response)
except Exception as e:
response = json_response(_sage_const_5 , ', "Error Message": "%s"' % e)
So, the service takes JSON request containing x, y, c, d and groupID and checks if:
$$X = (x, y) = c*P + d*Q$$
If the above condition is not satisfied, then JSON response simply contains an error message saying “Value mismatch! X != c*P + d*Q”. If the condition is satisfied then it calls get_response() function, which we will cover next.
Since we know that server communicates with the user only through JSON requests and JSON responses, we can write a function that takes in x, y, c, d, groupID and returns a request in JSON format, to be sent to the service as input:
def json_input(x, y, c, d, groupID):
dict1 = {'x': x, 'y': y, 'c': c, 'd': d, 'groupID': groupID}
return json.dumps(dict1)
Next, we analyse get_response:
# Teams should choose a non-guessable groupID
def get_response(x, y, c, d, groupID):
# open connection to database
conn = sqlite3.connect("points.db")
conn.row_factory = sqlite3.Row
conn_cursor = conn.cursor()
# convert sage integers to string to avoid "Python int too large for SQLite INTEGER"
x = str(x)
y = str(y)
c = str(c)
d = str(d)
# Select records that map to the same X value
conn_cursor.execute("SELECT * FROM points WHERE x = :x", {"x": x})
query = conn_cursor.fetchall()
# No record found -> Point is not yet included
if len(query) == _sage_const_0 :
# Insert point into database
conn_cursor.execute("INSERT INTO points (x, y, c, d, groupID) VALUES (?, ?, ?, ?, ?)",
(x, y, c, d, groupID))
# Get number of points added by this group
conn_cursor.execute("SELECT x FROM points WHERE groupID = :gID", {"gID": groupID})
points_found = conn_cursor.fetchall()
add_param = ', "points_found": %d' % len(points_found)
# When they found POINT_TRESHOLD distinguished points and a collision occured, return the colliding values as well
if len(points_found) > POINT_TRESHOLD:
add_param += ', "flag1": "%s"' % FLAG1
if server.collision_found:
# compute x from the collision, second flag is just x (not in flag format)
add_param += ', "collision": %s' % (server.collision)
response = json_response(_sage_const_0 , add_param)
else:
# One (or more) records found -> check if they have the same exponents
is_included = False
for row in query:
if row["c"] == c and row["d"] == d:
is_included = True
response = json_response(_sage_const_2 )
break
if not is_included:
# Exponents are different -> Collision found, add this point
conn_cursor.execute("INSERT INTO points (x, y, c, d, groupID, collision) VALUES (?, ?, ?, ?, ?, 1)",
(x, y, c, d, groupID))
# Get number of points added by this group
conn_cursor.execute("SELECT x FROM points WHERE groupID = :gID", {"gID": groupID})
points_found = conn_cursor.fetchall()
add_param = ', "points_found": %d' % len(points_found)
# add collision
server.collision_found = True
server.collision = '{"c_1": %s, "d_1": %s, "c_2": %s, "d_2": %s}' % (c, d, row["c"], row["d"])
if len(points_found) > POINT_TRESHOLD:
add_param += ', "collision": %s' % (server.collision)
else:
add_param += ', "collision": "collision found but not enough distinguished points submitted yet"'
response = json_response(_sage_const_1 , add_param + ', "c": %s, "d": %s' % (row["c"], row["d"]))
# close db connection and return response
conn.commit()
conn_cursor.close()
conn.close()
return response
get_response does the following:
- Selects all rows from the database points.db that have the same value of x and checks if there exists any record that contains the same record ie. it checks if len(query) == 0
- If the condition is true (there already exist records having same x), it checks whether c and d are same for the similar records found in step-1.
- If true, then an exact same input already exists in the database and hence it throws a JSON response “Point already included“.
- If false, then a collision is found. This implies that for a particular value of point
X, we have found two pairs of exponents such that- \(X = c_1*P + d_1*Q = c_2*P + d_2*Q\)
- Service adds this point to the database.
- It then calculates all x for which the groupID is same and assigns points_found = # x found.
- The counter points_found increases by one if a collision is found for a particular value of X. It checks if points_found > 200 and displays output according to that (which does not affect our exploit since we only want points_found > 200 at some point of time, to get the flag)
- If the condition is false (point X is not present in the database)
- Add the input points to the database
- It then calculates all x for which the groupID is same and assigns points_found = # x found
- It then checks if points_found > 200.
- If true then it displays the flag for our challenge!
The Exploit
We know from the property of Elliptic Curves that \(n*P = 0\), where n is the order of the subgroup generated by a point \(P\) on an Elliptic Curve. We can use this property to exploit this challenge. Let us see how:
If we set d = 0, $$\forall i\in \mathbb{I}, X = ((i*n+c)*P) + (0*Q) = ((i*n+c)*P)$$
We will now keep sending \(c, d\) as \((c, 0), (c+n, 0), (c+2n, 0), …, (c+200n, 0)\) having the same groupID (random enough to not collide with any other team’s groupID) and get 201 collisions which is just enough for us to get the flag. How? For the corresponding groupID, points_found = 201 > 200.
Then we send a random point on the curve having the same groupID as above and which is not there in the database. This will then pass the condition len(points_found) > 200 and give us the flag.
I wrote the script below to implement this attack in python. Note that ecauth is the python file I imported for doing Elliptic Curve operations:
import ecauth
import sqlite3
import json
from pwn import *
def json_input(x, y, c, d, groupID):
dict1 = {'x': x, 'y': y, 'c': c, 'd': d, 'groupID': groupID}
return json.dumps(dict1)
def create_curve():
p = 889774351128949770355298446172353873
a = 12345
b = 67890
curve = ecauth.CurveFp(p, a, b)
return curve
def base_point(curve, x, y, _order_point):
P = ecauth.Point(curve, x, y, _order_point)
return P
curve = create_curve()
_order_P = 79182553273022138539034276599687
_Px = 238266381988261346751878607720968495
_Py = 591153005086204165523829267245014771
P = base_point(curve, _Px, _Py, _order_P)
_Qx = 341454032985370081366658659122300896
_Qy = 775807209463167910095539163959068826
Q = base_point(curve, _Qx, _Qy, _order_P)
prev = 56558*P + 0*Q
for i in range(210):
r = remote("arcade.fluxfingers.net","1822")
param = i*_order_P
Point_x = (param + 56558)*P + 0*Q
assert prev.x() == Point_x.x() and prev.y() == Point_x.y()
data = json_input(Point_x.x(), Point_x.y(), param + 56558, 0, 888698063901)
r.send(data)
print i
print r.recv()
r.close()
r = remote("arcade.fluxfingers.net","1822")
Point_y = 35939*P + 11*Q
data2 = json_input(Point_y.x(), Point_y.y(), 35939, 11, 888698063901)
r.send(data2)
print r.recv()
r.close()
Running the above script gives us the flag!

Voila! It was fun!
However, this approach will not get us a flag for the Multiplayer Part-2 (Find out why)! Waiting for the challenge author to discuss the intended solution for Multiplayer Part-2.
UPDATE: Got the intended approach for both parts of this challenge: https://link.springer.com/content/pdf/10.1007%2F3-540-45537-X_17.pdf. Thanks to asante!